【アルゴリズム入門 Q009】市松模様

こんにちは。ECF代表のヒガです。

本記事では初心者向けアルゴリズムの演習問題を紹介しています。日頃のプログラミング学習にご活用ください。

はじめに

アルゴリズムとは、コンピューターに行わせる計算手順のことです。自在にプログラムを作るには、プログラム言語の文法の知識とともにアルゴリズムの考え方を身につけることが必要になります。

アルゴリズム技法習得の肝は「繰り返し」の活用です。この連載では、簡単な題材で繰り返しを使うアルゴリズムの基本パターンを練習していきます。

演習問題の一覧や勉強スタイルについてのアドバイスはこちらからどうぞ。

【プログラミング初心者向け】アルゴリズム入門演習問題集〜繰り返しをマスターしよう！

こんにちは。ECF代表のヒガです。プログラミング初心者向けアルゴリズム演習問題の連載記事まとめです。日頃のプログラミング学習、講義、研修等での演習にご活用ください。「繰り返しアルゴリズム」をマスターしようアルゴリズムとは、コンピューターに行...

Q009 市松模様

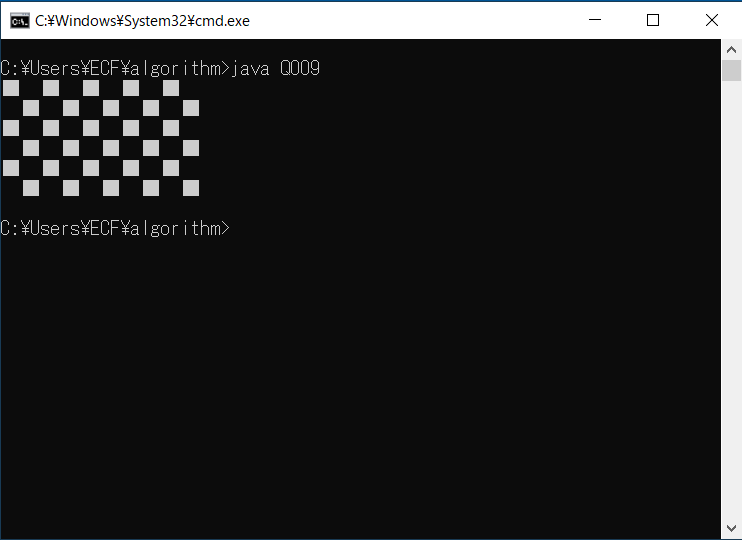
複数行にわたり文字「■」と文字「　」（全角スペース）を交互に並べて表示することで、実行例のような市松模様を表示させてください。ただし、行数や列数はプログラムの先頭で変数に代入することで指定してください。

行数に「6」、列数に「10」を指定した場合の実行例は次のとおりです。

ヒント

Q008の応用です。違いは、各行での列ループを始めるとき、文字の種類を適宜判断する必要があるということです。

解答例と解説

考え方

最初に「何を繰り返す」かを考えます。二重ループですので、小さな繰り返しと大きな繰り返しがあることに注目してください。小さな繰り返しは

文字'■'または'　'（全角スペース）を表示する

の繰り返しとなります。この繰り返しを行数分繰り返すのが大きな繰り返しです。つまり、

「文字'■'または'　'（全角スペース）を表示する」の繰り返し

を繰り返す、ということです。

ここまでは、Q008の縦ストライプと同じ考え方です。しかし今回の場合、各行の始まりの文字が行ごとに違っています。具体的には

奇数行目は'■'から開始して繰り返し（■　■　・・・）
偶数行目は'　'から開始して繰り返し（　■　■・・・）

という判断が各行の表示繰り返しで必要となります。Q008から考えると奇数行目の表示は

次の動作を列数分繰り返す
1. 今の繰り返しが奇数回目か偶数回目か判断する
  1. 奇数回目の場合、文字'■'を表示する
  2. 偶数回目の場合、文字'　'（全角スペース）を表示する

となり、偶数行目の表示は

次の動作を列数分繰り返す
1. 今の繰り返しが奇数回目か偶数回目か判断する
  1. 偶数回目の場合、文字'■'を表示する
  2. 奇数回目の場合、文字'　'（全角スペース）を表示する

となります。行の繰り返しも含めて全体を箇条書きしてみます。

行数と列数を指定する
次の動作を行数分繰り返す
1. 次の動作を列数分繰り返す
  1. 奇数行目か偶数行目か判断する
    1. 奇数行目の場合、今の繰り返しが奇数回目か偶数回目か判断する
      1. 奇数回目の場合、文字'■'を表示する
      2. 偶数回目の場合、文字'　'（全角スペース）を表示する
    2. 偶数行目の場合、今の繰り返しが奇数回目か偶数回目か判断する
      1. 偶数回目の場合、文字'■'を表示する
      2. 奇数回目の場合、文字'　'（全角スペース）を表示する
2. 改行する

という流れになります。

この段階でフローチャートやプログラムを作成してもOKですが、実はもうひと工夫できそうです。ここで言う工夫とは、考えたアルゴリズムをより短く、簡潔にするということです。アルゴリズムは基本的に簡潔な方が実装したときの実行速度が上がり、より効率のいいアルゴリズムであると評価されます。

文字'■'に着目すると、奇数行目のときは奇数回目、偶数行目のときは偶数回目に表示します。こうした共通部分に着目してうまく統合してしまいましょう。箇条書きの書き方を変えてみます。

行数と列数を指定する
次の動作を行数分繰り返す
1. 次の動作を列数分繰り返す
  1. 今の繰り返しが奇数回目か偶数回目か判断する
    1. 奇数行目の奇数回目または偶数行目の偶数回目の場合、文字'■'を表示する
    2. それ以外の場合、文字'　'（全角スペース）を表示する
2. 改行する

「奇数行目の奇数回目または偶数行目の偶数回目」の細かいロジックについては、変数をうまく使って実現することになりますので、フローチャートで解説します。

フローチャート例

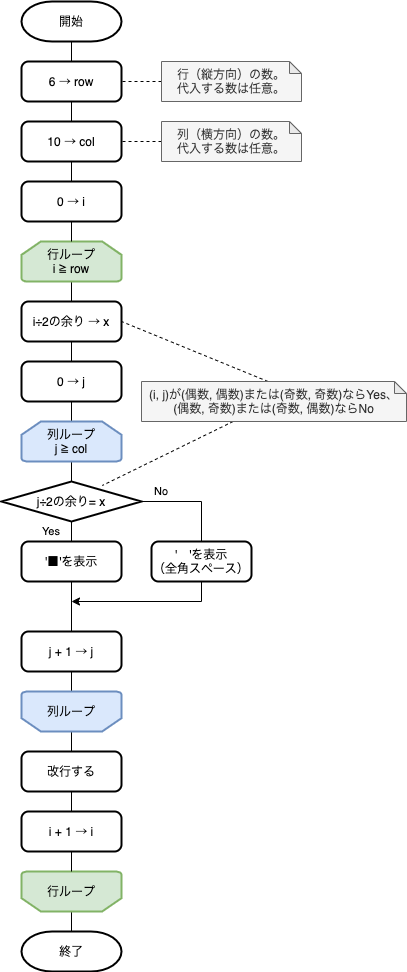
注目は変数xです。フローチャートでメモが書かれている2箇所で使われています。

変数xには変数iを2で割った余りが代入されています。変数iは行のことですので、

奇数行目の場合、xは1
偶数行目の場合、xは0

となります。この変数xの値を列ループの条件式の中で使います。条件式

j÷2の余り = x

は、jとiがともに奇数（2で割った余りが1同士）ならYes、jとiがともに偶数（2で割った余りが0同士）ならYesという意味です。これは考え方の箇条書きにあった「奇数行目の奇数回目または偶数行目の偶数回目の場合」に相当しています。

Javaでの実装例

public class Q009 {
    public static void main(String[] args) {
        int row = 6;  // 行（縦方向）の数
        int col = 10;  // 列（横方向）の数
        
        for (int i = 0; i < row; i++) {    // 行ループ
            int x = i % 2; // 偶数行の場合は0、奇数行の場合は1
            
            for (int j = 0; j < col; j++) {    // 列ループ
                // 偶数行の場合は偶数列が■、奇数行の場合は奇数列が■
                if (j % 2 == x) {
                    System.out.print('■');
                } else {
                    System.out.print('　'); // 全角スペースを表示
                }
            }
            System.out.println(); // 列ループが終われば改行
        }
    }
}

Q008のプログラム実装、そして上のフローチャートとの対応からプログラム実装例の流れを確認しましょう。だいぶ複雑になってきたので、プログラムには適宜コメントを入れるようにしましょう。

おわりに

実際にはアルゴリズム技術に慣れてから意識することではありますが、ある仕様を実現するアルゴリズムは無数にあったとしても、それぞれのアルゴリズムには良し悪しがあります。一旦目的のアルゴリズムを完成させたとしても、「まだ工夫できないか？」ということを考えることが大切です。初学者の段階でも意識付けておくといいでしょう。

次回はこちらです。