基本情報科目B対策（5章 サーチとソート）

基本情報技術者試験
2025.03.28

こんにちは、ECF Techブログ担当のmichiharu.Tです。

本記事は「基本情報技術者試験　科目B対策講座」の一部です。講座記事のすべてをご覧になりたい方は、下のリンクからご確認ください。

基本情報科目B対策講座（1章 はじめに）
はじめに本教材は基本情報技術者試験（科目B）の学習を目的とした教材です。試験合格のための学習にお役立て頂ければ幸いです。想定読者 基本情報技術者試験(科目A)を学習中、もしくは学習済の方 アルゴリズムやプログラミングの知識(科目A程度)をお...
tech.e3factory.com
2025.02.25

本章では代表的な探索（サーチ）アルゴリズムと並び替え（ソート）アルゴリズムを学びます。

5-1 サーチアルゴリズム

5-1-1 線形探索法

問題

[オリジナル問題]
　関数 search は、引数の値を配列 ary の中から探索し、一致する要素があればtrue、そうでなければfalseを返す関数です。プログラム中の空欄を埋めてください。

〔プログラム〕

大域: 整数型の配列: ary ← {8,12,33,15,20,6}

〇論理型: search(整数型: data)
  整数型: i
  for (i を 1 から aryの要素数 まで 1 ずつ増やす)
    if(  ①  )
      return true
    endif
  endfor
  return false

ヒント1

空欄①で、配列の各要素と引数dataが一致しているかを判定しています。配列の各要素の参照方法は3-1-1を参考にしてみましょう。

考え中

解答解説

〔解答〕
①：ary[i]＝data

〔解説〕
ary[i]＝dataと記述することで、配列の各要素をdataと比較することができます。配列の要素とdataの値が一致した場合にtrueを返しています。一致しなかった場合は、forループを抜けた後にfalseが返されます。

5-1-2 二分探索法(1)

問題

[オリジナル問題]
　関数 binarySearch は、引数の値を配列 ary の中から探索し、一致する要素があればtrue、そうでなければfalseを返す関数です。ただし、配列 ary は昇順に整列されているものとします。この関数をbinarySearch(25)で呼び出したとき、プログラム中のコメント①部分の処理は何回実行されるか答えてください。

〔プログラム〕

大域: 整数型の配列: ary ← {9,12,18,25,33,40}

〇論理型: binarySearch(整数型: data)
  整数型: start ← 1
  整数型: end ← aryの要素数
  整数型: middle

  while(start＞end)
    middle ← (start+end)÷2 /*小数点は切り捨て*/
    if(data ＝ ary[middle])
      return true
    elseif(data＜ary[middle])
      end ← middle-1 /* ① */
    else
      start ← middle+1
    endif
  return false

ヒント1

二分探索法のプログラムを読み解く問題です。

二分探索は値が見つかるまで、下のような処理を繰り返します。

  • startとendで示す探索範囲から、ほぼ真ん中の要素を対象にする。
  • 対象の要素が探している値と一致しているかを判断する。一致していれば終了。
  • 一致していなければ、探索範囲を狭める。

対象値が見つからない場合、最終的にstartとendの値が逆転しますので、これをくり返し処理終了の条件とします。

考え中

解答解説

〔解答〕
　1回

〔解説〕
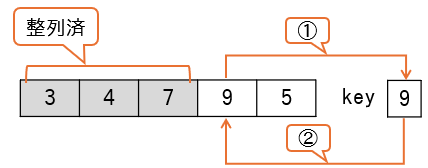
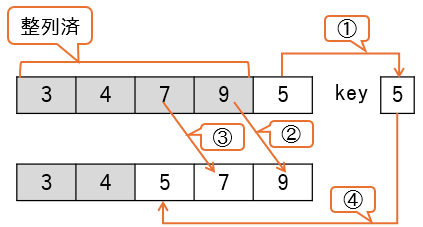
　プログラムをトレースしてみましょう。変数startの初期値は1、endの初期値は配列の要素数である6です。したがって、初期状態は図のようになります。変数startとendは配列の要素番号として用いるので、図では矢印で表しています。

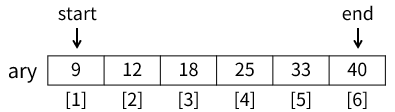
5-1-2 トレース1

whileループから処理を続けます。9行目middle ← (start+end)÷2は 1+6÷2 で 3.5、小数点切り捨てで 3 となり、middleには 3 が代入されます（下図）。

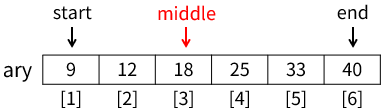
5-1-2 トレース2

ary[middle]は18で、dataの値は引数である25です。ifの条件式data ＝ ary[middle]、およびelseifの条件式data＜ary[middle]のいずれにも該当しません。よって、else部分のstart ← middle+1が実行され、変数startは4となります。これにより、探索範囲は要素番号4～6に絞られます（下図）。

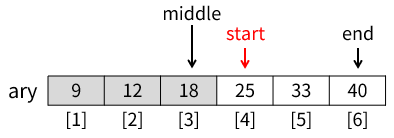
5-1-2 トレース3

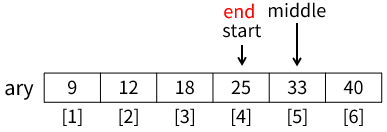
再度9行目の処理となります。middle ← (start+end)÷2は 4+6÷2 で 5、middleには 5 が代入されます（下図）。

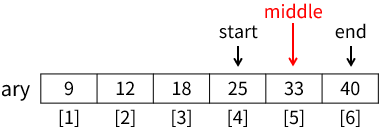
5-1-2 トレース4

ary[middle]は33なので、elseifの条件式data＜ary[middle]が true となり、コメント①部分が実行されます。処理はend ← middle-1なので、変数endは4となり、startとendは同じ値になります（下図）。

5-1-2 トレース5

再度9行目の処理となります。middle ← (start+end)÷2は 4+4÷2 で 4、middleには 4 が代入されます（下図）。

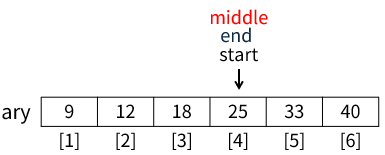
5-1-2 トレース6

ary[middle]は25なので、ifの条件式が true となり、戻り値としてtrueを返し、処理を終了します。以上が二分探索法の基本的な動きになります。

結果、空欄①部分が実行されたのは1回となります。

5-1-3 二分探索法(2)

問題

[出典：基本情報技術者試験 科目B サンプル問題 問13]
次の記述中のに入れる正しい答えを、解答群の中から選べ。ここで、配列の要素番号は 1 から始まる。

　関数 search は、引数 data で指定された配列に、引数 target で指定された値が含まれていればその要素番号を返し、含まれていなければ -1 を返す。data は昇順に整列されており、値に重複はない。
　関数 search には不具合がある。例えば、dataのの場合は、無限ループになる。

〔プログラム〕

〇整数型: search(整数型の配列: data, 整数型: target)
　整数型: low, high, middle

  low ← 1
  high ← dataの要素数

  while (low ≦ high)
    middle ← (low + high) ÷ 2 の商
    if (data[middle] ＜ target)
      low ← middle
    elseif (data[middle] ＞ target)
      high ← middle
    else
      return middle
    endif
  endwhile

  return -1

解答群
　ア　要素数が1で、targetがその要素の値と等しい
　イ　要素数が2で、targetがdataの先頭要素の値と等しい
　ウ　要素数が2で、target がdataの未尾要素の値と等しい
　工　要素に-1が含まれている

ヒント1

各選択肢の状況を持つ配列を自作し、トレースしてみましょう。たとえば選択肢アであれば targetは5、配列dataの内容は{5}となります。

考え中

解答解説

〔解答〕
　ウ

〔解説〕
選択肢アから動作を確認してみましょう。各トレースの図は、次のようになっています。

  • 実行された処理のみを示しています。
  • low,high,middle,target,data列は各変数の処理時の値を示しています。
  • 条件式がある処理では、条件式の判定結果が判定列に記載されています。
  • 処理に関連する変数は強調表示しています。

選択肢ア
例として、配列dataの内容を{5}、targetを5 でトレースを進めます。

処理 low high middle target data 判定
while (low ≦ high) 1 1 - 5 {5} true
middle ← (low + high) ÷ 2 の商 1 1 1 5 {5} -
if (data[middle] ＜ target) 1 1 1 5 {5} false
elseif (data[middle] ＞ target) 1 1 1 5 {5} false
return middle 1 1 1 5 {5} -

ifおよびelseifの処理に入ることなく、else部分でreturn文が実行され、プログラムが終了します。

選択肢イ
例として、data={5,8}、target=5でトレースを進めます。

処理 low high middle target data 判定
while (low ≦ high) 1 2 - 5 {5,8} true
middle ← (low + high) ÷ 2 の商 1 2 1 5 {5,8} -
if (data[middle] ＜ target) 1 2 1 5 {5,8} false
elseif (data[middle] ＞ target) 1 2 1 5 {5,8} false
return middle 1 2 1 5 {5,8} -

ifおよびelseifの処理に入ることなく、else部分でreturn文が実行され、プログラムが終了します。

選択肢ウ
例として、data={3,5}、target=5でトレースを進めます。

処理 low high middle target data 判定
while (low ≦ high) 1 2 - 5 {3,5} true
middle ← (low + high) ÷ 2 の商 1 2 1 5 {3,5} -
if (data[middle] ＜ target) 1 2 1 5 {3,5} true
low ← middle 1 2 1 5 {3,5} -

上記の流れで処理が行われた後、再びwhile文の先頭に戻ります。lowとhighの値が変化していないため、2回目のループも上図とまったく同じ処理の流れとなり、無限ループとなります。こちらが正解の選択肢です。

選択肢エ
例として、data={-1, 3}、target=-1でトレースを進めます。

処理 low high middle target data 判定
while (low ≦ high) 1 2 - -1 {-1,3} true
middle ← (low + high) ÷ 2 の商 1 2 1 -1 {-1,3} -
if (data[middle] ＜ target) 1 2 1 -1 {-1,3} false
elseif (data[middle] ＞ target) 1 2 1 -1 {-1,3} false
return middle 1 2 1 -1 {-1,3} -

return文が実行され、プログラムが終了します。

結果、選択肢ウのみが無限ループになってしまうことがわかります。

5-2 ソートアルゴリズム

5-2-1 バブルソート(1)

問題

[オリジナル問題]　
　関数 bubbleSort は、引数で指定された配列の要素を昇順に並び変える関数です。この関数をbubbleSort({8,3,5,7,4})で呼び出した場合、プログラム中のコメント①の行は何回実行されるか答えてください。

〔プログラム〕

〇bubbleSort(整数型配列: ary)
  整数型: i
  整数型: j
  整数型: n ← aryの要素数ー1
  整数型: work
  for(i を 1 から aryの要素数ー1 まで 1 ずつ増やす)
    for(j を 1 から n まで 1 ずつ増やす)
      if(ary[j]>ary[j+1])
        work ← ary[j]
        ary[j] ← ary[j+1]　/*①*/
        ary[j+1] ← work
      endif
    endfor
    n ← n - 1
  endfor

基礎知識

バブルソートは隣同士の要素を比較し、順番が逆の場合に要素を入れ替えるソートアルゴリズムです。次の目的で二重ループを用います。

  • 外側のループ：1回で1つ値が確定する。
  • 内側のループ：隣同士の比較をくり返す。

ヒント1

問題文の配列を例に外側ループ最初の1回の動きを、下のトレース表で確認しましょう。9～11行目の値の入替処理は1つの行で示しています。

処理 i j ary 判定
if(ary[j]>ary[j+1]) 1 2 {8,3,5,7,4} true
work ← ary[j]
ary[j] ← ary[j+1]
ary[j+1] ← work		 1 2 {3,8,5,7,4}
if(ary[j]>ary[j+1]) 1 3 {3,8,5,7,4} true
work ← ary[j]
ary[j] ← ary[j+1]
ary[j+1] ← work		 1 3 {3,5,8,7,4}
if(ary[j]>ary[j+1]) 1 4 {3,5,8,7,4} true
work ← ary[j]
ary[j] ← ary[j+1]
ary[j+1] ← work		 1 4 {3,5,7,8,4}
if(ary[j]>ary[j+1]) 1 5 {3,5,7,8,4} true
work ← ary[j]
ary[j] ← ary[j+1]
ary[j+1] ← work		 1 5 {3,5,7,4,8}

最大値の8が、最後の要素に向かって移動していることがわかります。これで最後の要素の値が確定します。

上記の操作をあと3回くり返すことで、後ろの要素から値が確定することになります。残りの動きはていねいにトレースを進めて、答えを導き出しましょう。

考え中

解答解説

〔解答〕
　6回

〔解説〕
外側forループの変数iが2以降のトレースは次のようになります。

iが2の時

処理 i j ary 判定
if(ary[j]>ary[j+1]) 1 2 {3,5,7,4,8} false
if(ary[j]>ary[j+1]) 1 3 {3,5,7,4,8} false
if(ary[j]>ary[j+1]) 1 4 {3,5,7,4,8} true
work ← ary[j]
ary[j] ← ary[j+1]
ary[j+1] ← work		 1 4 {3,5,4,7,8}

2番目に大きい7が移動し、4番目の要素の値が確定します。

iが3の時

処理 i j ary 判定
if(ary[j]>ary[j+1]) 1 2 {3,5,4,7,8} false
if(ary[j]>ary[j+1]) 1 3 {3,5,4,7,8} true
work ← ary[j]
ary[j] ← ary[j+1]
ary[j+1] ← work		 1 3 {3,4,5,7,8}

3番目に大きい5が移動し、3番目の要素の値が確定します。

iが4の時

処理 i j ary 判定
if(ary[j]>ary[j+1]) 1 2 {3,4,5,7,8} false

移動は発生しません。2番目の要素の値が確定します。結果としてすべての値が昇順に並びます。

入替処理はヒント1で示した4回も加えて、合計6回発生していることがわかります。

5-2-2 バブルソート(2)

[オリジナル問題]　

　関数 bubbleSort は、引数で指定された配列の要素を昇順に並び変える関数です。プログラム中の空欄①に当てはまるものを解答群から選んでください。

〔プログラム〕

〇bubbleSort(整数型配列: ary)
  整数型: i
  整数型: j
  整数型: work
  for(i を 1 から aryの要素数ー1 まで 1 ずつ増やす)
    for(j を aryの要素数 から ① まで 1 ずつ減らす)
      if(ary[j-1]>ary[j])
        work ← ary[j-1]
        ary[j-1] ← ary[j]
        ary[j] ← work
      endif
    endfor
  endfor

解答群
ア　0　　イ　1　　ウ　i　　エ　i＋1

ヒント1

5-2-1の問題と異なり、最初の要素の値から決定していくアルゴリズムになっています。実際の値を使って、外側のfor文1回分程度のトレースを行ってみましょう。

考え中

解答解説

〔解答〕
①：エ

〔解説〕
引数aryに{8,5,3,7,4}が与えられたものとして、トレースをしてみましょう。iが1の時のforループは次のようになります。

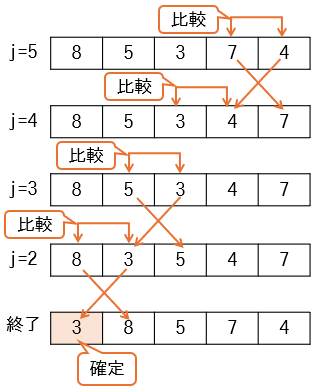
5-2-2 トレース1

jが2になるまでくり返しを行うと、最小値が最初の要素に移動することがわかります。空欄①の答えの1つとして2が考えられますが、解答群にありません。残りの解答群で2の代わりとなりうるのは、i＋1のみになります。iの値が1なのでi＋1は2となります。

空欄①にi＋1を設定したものとして、iが2の時の内側ループの動きを確認すると、次のようになります。

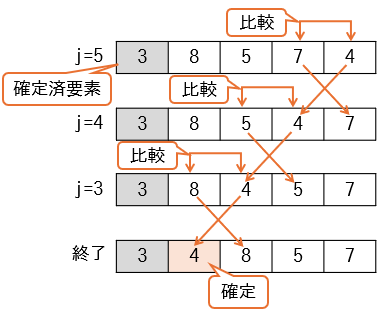
5-2-2 トレース2

iは2、jはi+1で3までくり返し処理を行います。上図のとおり、要素番号2の位置に次に小さい値である4が設定されて終了することがわかります。

5-2-3 挿入ソート(1)

問題

[オリジナル問題]　

　関数 insertionSort は、引数で指定された配列の要素を昇順に並び変える関数です。プログラム中の空欄を埋めてください。

〔プログラム〕

〇整数型の配列: insertionSort(整数型配列: ary)
  整数型: i
  整数型: j
  整数型: key

  for (i を 2 から aryの要素数 まで 1 ずつ増やす)
    key ← ary[i]
    j ← ①
    while (j ≧ 1 and ary[j] ＞ key)
      ary[j + 1] ← ary[j]
      j ← j - 1
    endwhile
    ary[②] ← key
  endfor
  return ary

解答群
　ア　1　　イ　i　　ウ　i＋1　　エ　iー1　　オ　j　　カ　j＋1

基礎知識

挿入ソートは、整列済みの配列の適切な位置に新しい要素を追加していく。という考え方で並びかえを実現する方法です。たとえば、次のような配列を昇順に並び変えたいとします。

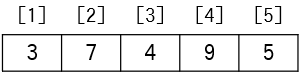
5-2-3 トレース1

この時、最初の要素を整列済とみなし、2番目の要素である7をどこに挿入するかを決定します。

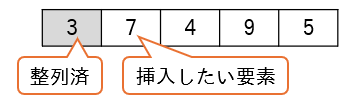
5-2-3 トレース2

7は3より大きいため、3の後ろに挿入され（2番目の要素の値は変わらない）、最初の2つの要素は整列済となります。

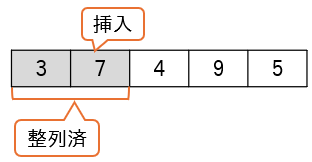
5-2-3 トレース3

次に3番目の要素である4をどこに挿入するかを決定します。

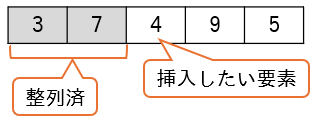
5-2-3 トレース4

4は7の前に挿入したいので、7を1つ後ろにずらして4を挿入します。

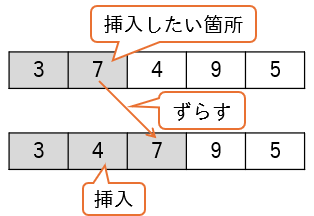
5-2-3 トレース5

このような処理を、未整列の要素が無くなるまでくり返すことで並び替えを完了します。

ヒント1

while文は、挿入する要素より大きな値を後ろにずらす処理を行っています。

考え中

解答解説

〔解答〕
①：エ
②：カ

〔解説〕
　下のような配列を例に動作を考えてみましょう。

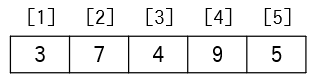
5-2-3 トレース6

以下、iの値ごとにトレース表とイメージ図を示しています。トレース表中の図列は図の〇つき番号と対応しています。

i=2の時

処理 key i j ary 判定 図
key ← ary[i] 7 2 - {3,7,4,9,5} - ①
j ← iー1 7 2 1 {3,7,4,9,5} - -
while (j ≧ 1 and ary[j] ＞ key) 7 2 1 {3,7,4,9,5} false -
ary[j＋1] ← key 7 2 1 {3,7,4,9,5} - ②

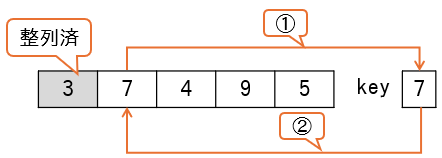
5-2-3 トレース6

変数keyは挿入対象の値で7です。整列済要素に7より大きい値はないため、最終的に2番目に挿入されます。結果、7の位置は変化しません。

i=3の時

処理 key i j ary 判定 図
key ← ary[i] 4 3 - {3,7,4,9,5} - ①
j ← iー1 4 3 2 {3,7,4,9,5} - -
while (j ≧ 1 and ary[j] ＞ key) 4 3 2 {3,7,4,9,5} true -
　ary[j + 1] ← ary[j] 4 3 2 {3,7,7,9,5} - ②
　j ← j - 1 4 2 1 {3,7,7,9,5} - -
while (j ≧ 1 and ary[j] ＞ key) 4 2 1 {3,7,7,9,5} false -
ary[j＋1] ← key 4 2 1 {3,4,7,9,5} - ③

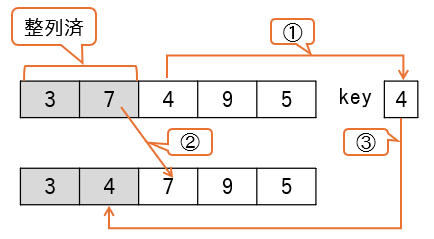
5-2-3 トレース6

挿入対象の値は4です。4は3と7の間に入る必要がありますので、while文内で7を後ろにずらしています。

i=4の時

処理 key i j ary 判定 図
key ← ary[i] 9 4 - {3,4,7,9,5} - ①
j ← iー1 9 4 3 {3,7,4,9,5} - -
while (j ≧ 1 and ary[j] ＞ key) 9 4 3 {3,4,7,9,5} false -
ary[j＋1] ← key 9 4 3 {3,4,7,9,5} - ②

5-2-3 トレース6

変数keyは挿入対象の値で9です。整列済要素に9より大きい値はないため、最終的に4番目に挿入されます。結果、9の位置は変化しません。

i=5の時

処理 key i j ary 判定 図
key ← ary[i] 5 5 - {3,4,7,9,5} - ①
j ← iー1 5 5 4 {3,4,7,9,5} - -
while (j ≧ 1 and ary[j] ＞ key) 5 5 4 {3,4,7,9,5} true -
　ary[j + 1] ← ary[j] 5 5 4 {3,4,7,9,9} - ②
　j ← j - 1 5 5 3 {3,4,7,9,9} - -
while (j ≧ 1 and ary[j] ＞ key) 5 5 3 {3,4,7,9,9} true -
　ary[j + 1] ← ary[j] 5 5 3 {3,4,7,7,9} - ③
　j ← j - 1 5 5 2 {3,4,7,7,9} - -
while (j ≧ 1 and ary[j] ＞ key) 5 5 2 {3,4,7,7,9} false -
ary[j＋1] ← key 5 5 2 {3,4,5,7,9} - ④

5-2-3 トレース6

挿入対象の値は5です。5は4と7の間に入る必要がありますので、while文内で7と9を後ろにずらしています。最後にkeyの値を3番目の要素に挿入しています。

5-2-4 挿入ソート(2)

問題

[オリジナル問題]　

　関数 insertionSort は、引数で指定された配列の要素を昇順に並び変える関数です。この関数をinsertionSort({5,2,8,3,4})で呼び出したとき、プログラム中のコメント①は何回実行されるか答えてください。

〔プログラム〕

〇整数型の配列: insertionSort(整数型配列: ary)
  整数型: i
  整数型: j
  整数型: key

  for (i を 1 から aryの要素数 まで 1 ずつ増やす)
    key ← ary[i]
    j ← iー1
    while (j ≧ 0 and ary[j]＞key)
      ary[j + 1] ← ary[j] /*①*/
      j ← j - 1
    endwhile
    ary[j＋1] ← key
  endfor
  return ary

ヒント1

5-2-3のプログラムに正しい答えが入った状態で動作させています。トレースしながら、①の実行回数を数えていきましょう。

考え中

解答解説

〔解答〕
　5回

〔解説〕
各forループごとの動きを見ていきましょう。i=2から確認します。

i=2の時
最初の要素を整列済とみなし、2番目の要素をどこに挿入するかを決めます。

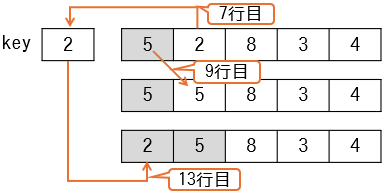
5-2-4 トレース1

  • 7行目key ← ary[i]で、変数keyに2が代入されます。
  • while文中のary[j + 1] ← ary[j]は1回実行され、5が後ろにずれます。
  • 11行目ary[j＋1] ← keyで、1番目の要素にkeyの値が代入されます。

i=3の時
先頭2つの要素を整列済とみなし、3番目の要素をどこに挿入するかを決めます。

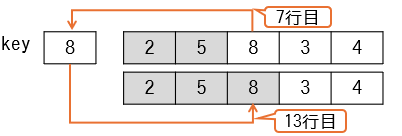
5-2-4 トレース2

  • 7行目key ← ary[i]で、変数keyに8が代入されます。
  • 整列済の要素はすべて8より小さいためwhile文中のary[j + 1] ← ary[j]は行われません。
  • 11行目ary[j＋1] ← keyで、3番目の要素にkeyの値が代入されます。変化はありません。

i=4の時
先頭3つの要素を整列済とみなし、4番目の要素をどこに挿入するかを決めます。

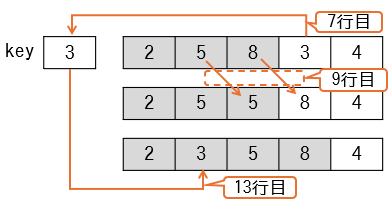
5-2-4 トレース3

  • 7行目key ← ary[i]で、変数keyに3が代入されます。
  • while文中のary[j + 1] ← ary[j]は2回実行され、5と8が後ろにずれます。
  • 11行目ary[j＋1] ← keyで、2番目の要素にkeyの値が代入されます。

i=5の時
先頭4つの要素を整列済とみなし、5番目の要素をどこに挿入するかを決めます。

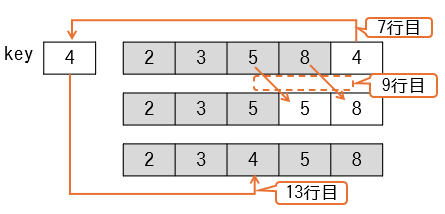
5-2-4 トレース4

  • 7行目key ← ary[i]で、変数keyに3が代入されます。
  • while文中の9ary[j + 1] ← ary[j]は2回実行され、5と8が後ろにずれます。
  • 11行目ary[j＋1] ← keyで、3番目の要素にkeyの値が代入されます。

プログラム中の①が行われた回数は、全部で5回となります。

5-2-5 選択ソート(1)

問題

[オリジナル問題]　

　関数 selectionSort は、引数で指定された配列の要素を昇順に並び変える関数です。プログラム中の空欄を埋めてください。

〔プログラム〕

〇整数型配列: selectionSort(整数型配列: ary)
  整数型: i
  整数型: j
  整数型: min
  整数型: wk

  for (i を 1 から aryの要素数 ー 1 まで 1 ずつ増やす)
    min ← i
    for (j を i ＋ 1 から aryの要素数 まで 1 ずつ増やす)
      if (ary[j] ＜ ary[min])
        min = ①;
      endif
    endfor

    if (min ≠ i)
      wk ← ary[i]
      ary[i] ← ary[min]
      ary[min] ← ②
    endif
  endfor
  return ary

基礎知識

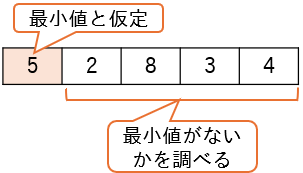
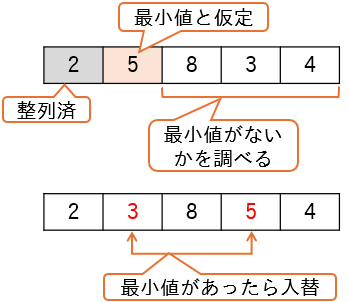
選択ソートで配列要素を昇順に並べる場合は、次のようにします。

最初の要素を最小値と仮定し、残りの要素から最小値になるべき値があるかどうかをチェックします。

5-2-5 説明1

最小値が見つかれば、最小値と仮定した要素と入れ替えます。

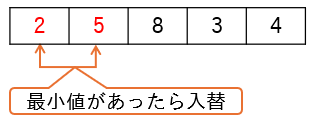
5-2-5 説明2

以降の要素についても同様の処理をくり返します。

5-2-5 説明3

考え中

解答解説

〔解答〕

①：j
②：wk

〔解説〕

次のような配列を例に、動作を追いかけてみましょう。

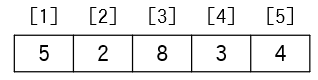
5-2-5 トレース1

i=1の時

処理 min i j ary 判定
min ← i 1 1 - {5,2,8,3,4} -

min ← iで、変数minとiは共に1となります。内側ループの変数jはi+1から始まりますので2です。下図のようになります。変数i,j,minはそれぞれ要素番号を示すため、図では矢印で示しています。

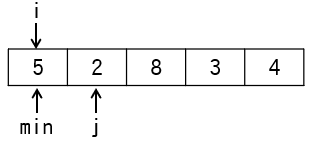
5-2-5 トレース2

処理 min i j ary 判定
if (ary[j] ＜ ary[min]) 1 1 2 {5,2,8,3,4} true

if文の条件式ary[j] ＜ ary[min]で値の大小を比較します。jが指す要素が小さい場合はjが新たな最小値となるため、変数jを変数minに代入する必要があります。よって空欄①は j となります。

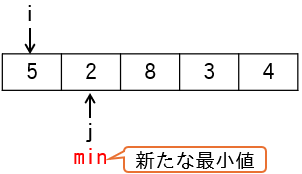
処理 min i j ary 判定
min = j 2 1 2 {5,2,8,3,4} -

変数jの値がminに代入され、下図のようになります。

5-2-5 トレース3

変数jはaryの要素数まで1ずつ増えますので、残りの要素の大小比較も行います。

処理 min i j ary 判定
if (ary[j] ＜ ary[min]) 2 1 3 {5,2,8,3,4} false
if (ary[j] ＜ ary[min]) 2 1 4 {5,2,8,3,4} false
if (ary[j] ＜ ary[min]) 2 1 5 {5,2,8,3,4} false

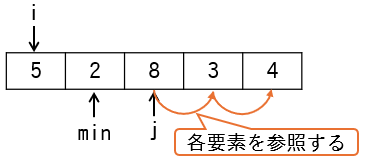
5-2-5 トレース4

ですが、以降の要素の中には2より小さい値は存在しないため、そのまま内側のループを終了します。

処理 min i j ary 判定
if (min ≠ i) 2 1 2 {5,2,8,3,4} -

min ≠ iの比較において変数minとiの値は異なるため、if文内の入替処理が行われます（下図）。16～18行目は値の入替処理を行っているため、空欄②は wk となります。

処理 min i j ary 判定
wk ← ary[i]
ary[i] ← ary[min]
ary[min] ← wk		 2 1 2 {2,5,8,3,4} -

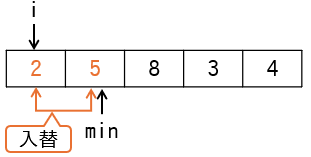
5-2-5 トレース5

変数iと変数minが指す要素の入替処理が行われています。

i=2の時

処理 min i j ary 判定
min ← i 2 2 - {2,5,8,3,4} -
if (ary[j] ＜ ary[min]) 2 2 3 {2,5,8,3,4} false

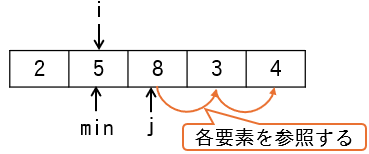
5-2-5 トレース6

iが2の時は、minが2、jが3から始まります。jは各要素を上図のように参照していきます。

処理 min i j ary 判定
if (ary[j] ＜ ary[min]) 2 2 4 {2,5,8,3,4} true
min = j 4 2 4 {2,5,8,3,4} -

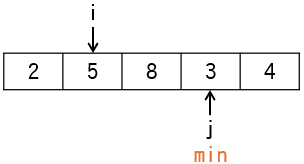
5-2-5 トレース7

jが4の時、条件式ary[j] ＜ ary[min]がtrueとなり、minに4が代入されます（上図）。

処理 min i j ary 判定
if (ary[j] ＜ ary[min]) 2 2 5 {2,5,8,3,4} false

以降、3よりも小さい値は無いため、そのまま内側ループを抜けます。

処理 min i j ary 判定
if (min ≠ i) 4 2 2 {2,5,8,3,4} -
wk ← ary[i]
ary[i] ← ary[min]
ary[min] ← wk		 4 2 2 {2,3,8,5,4} -

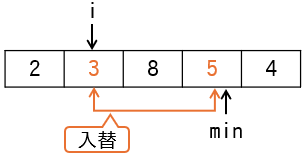
5-2-5 トレース8

min ≠ iの比較が行われます。変数minとiの値は異なるため、if文内の入替処理が行われます（上図）。

以降、iが3および4の時のトレース表です。

i=3の時

処理 min i j ary 判定
min ← i 3 3 - {2,3,8,5,4} -
if (ary[j] ＜ ary[min]) 3 3 4 {2,3,8,5,4} true
min = j 4 3 4 {2,3,8,5,4} -
if (ary[j] ＜ ary[min]) 4 3 5 {2,3,8,5,4} true
min = j 5 3 5 {2,3,8,5,4} -
if (min ≠ i) 5 3 - {2,3,8,5,4} true
wk ← ary[i]
ary[i] ← ary[min]
ary[min] ← wk		 5 3 - {2,3,4,5,8} -

i=4の時

処理 min i j ary 判定
min ← i 4 4 - {2,3,4,5,8} -
if (ary[j] ＜ ary[min]) 4 4 5 {2,3,4,5,8} true
min = j 5 4 5 {2,3,4,5,8} -
if (min ≠ i) 5 4 - {2,3,4,5,8} true
wk ← ary[i]
ary[i] ← ary[min]
ary[min] ← wk		 5 4 - {2,3,4,5,8} -

以上でプログラムが終了し、配列aryが昇順に並んでいることが確認できます。

5-2-6 選択ソート(2)

問題

[オリジナル問題]　

　関数 selectionSort は、引数で指定された配列の要素を昇順に並び変える関数です。この関数をselectionSort({3,7,4,8,1})で呼び出したとき、プログラム中のコメント①は何回実行されるか答えてください。

〔プログラム〕

〇整数型配列: selectionSort(整数型配列: ary)
  整数型: i
  整数型: j
  整数型: min
  整数型: wk

  for (i を 1 から aryの要素数 ー 1 まで 1 ずつ増やす)
    min ← i
    for (j を i ＋ 1 から aryの要素数 まで 1 ずつ増やす)
      if (ary[j] ＜ ary[min])
        min = j;
      endif
    endfor

    if (min ≠ i)
      wk ← ary[i]
      ary[i] ← ary[min] /*①*/
      ary[min] ← wk
    endif
  endfor
  return ary

ヒント1

5-2-5のプログラムに正しい答えが入った状態で動作させています。トレースしながら、①の実行回数を数えていきましょう。

考え中

解答解説

〔解答〕

　3回

〔解説〕

外側のループの各回ごとの動作を確認しましょう。

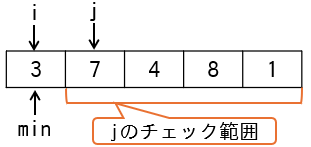
i=1の時

jは2,minは1から始まります。変数jは1ずつ加算され、配列の2番目以降の要素からminより小さい値を探します（下図）。

5-2-6 トレース1

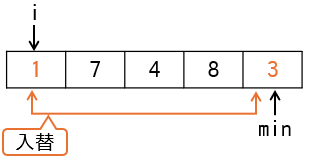
1番目の要素3より小さい値は、最後の要素1ですので、内側ループを抜けた時点でminは5となり、16～18行目の入替処理で1と3が入れ替わります（下図）。

5-2-6 トレース2

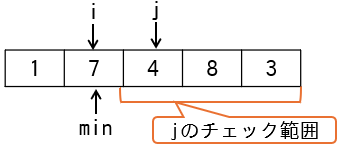
i=2の時

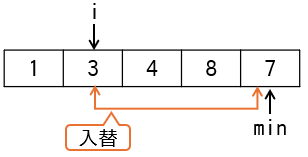
jは3,minは2から始まります。変数jは1ずつ加算され、配列の3番目以降の要素からminより小さい値を探します（下図）。

5-2-6 トレース3

2番目の要素7より小さい値のうち最小の値は、最後の要素3ですので、内側ループを抜けた時点でminは5となり、16～18行目の入替処理で7と3が入れ替わります（下図）。

5-2-6 トレース4

i=3の時

jは4,minは3から始まります。変数jは1ずつ加算され、配列の4番目以降の要素からminより小さい値を探します（下図）。

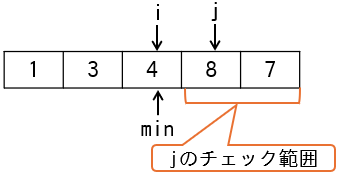
5-2-6 トレース5

3番目の要素4より小さい値は以降の要素に存在しないため、入替処理は発生しません。

i=4の時

jは5,minは4から始まります。変数jは1ずつ加算され、配列の5番目の要素がminより小さいかどうかをチェックします（下図）。

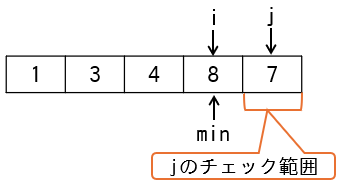
5-2-6 トレース6

4番目の要素8より小さい値は、最後の要素7ですので、内側ループを抜けた時点でminは5となり、16～18行目の入替処理で8と7が入れ替わります（下図）。

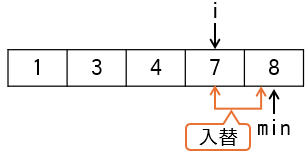
5-2-6 トレース7

これでソートが完了です。コメント/* ① */部分の処理回数は、入替が発生した回数に等しいので正解は3回となります。

5-2-7 クイックソート

問題

[出典：基本情報技術者試験 令和5年 科目B 問3]

　次の記述中のに入れる正しい答えを、解答群の中から選べ。ここで、配列の要素番号は1から始まる。

　次の手続sortは、大域の整数型の配列dataの、引数 first で与えられた要索番号から引数 last で与えられた要素番号までの要素を昇順に整列する。ここで、first ＜ last とする。手続sortをsort(1, 5)として呼び出すと、/*** α ***/の行を最初に実行したときの出力は“”となる。

〔プログラム〕

大域：整数型の配列：data ← {2，1, 3, 5, 4}

〇sort(整数型： first，整数型: last)
　整数型：pivot,i，j
　pivot ← data[(first + last) ÷ 2 の商]
　i ← first
　j ← last

　while (true)
  　while (data[i] ＜ pivot)
      i ← i ＋ 1
    endwhile
    while (pivot ＜ data[j])
      j ← j ー 1
    endwhile
    if (i ≧ j)
      繰返し処理を終了する
    endif
    data[i]とdata[j]の値を入れ替える
    i ← i ＋ 1
    j ← j ー 1
  endwhile
  dataの全要素の値を要索番号の順に空白区切りで出力する /*** α ***/
  if (first ＜ i ー 1)
    sort(first, i ー 1)
  endif
  if (j ＋ 1 ＜ last)
    sort (j ＋ 1, last)
  endif

解答群
　ア　1 2 3 4 5　　イ　1 2 3 5 4
　ウ　2 1 3 4 5　　エ　2 1 3 5 4

基礎知識

ソートの名称は明示していませんが、クイックソートを基本にした問題です。クイックソートは再帰の考え方を使って、次のような方法で値を並び替えます。

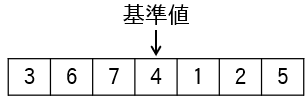
下の配列を対象に、昇順に並び替える際の動作について説明します。

5-2-7 トレース1

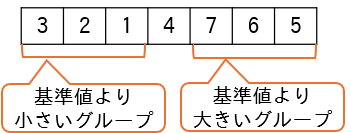
(1)基準値を決めます。

5-2-7 トレース2

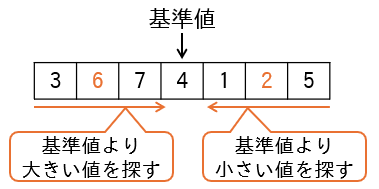
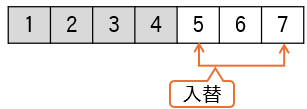
(2)基準値より大きい値を左から右に向かって探し、基準値より小さい値を右から左に向かって探します。

5-2-7 トレース3

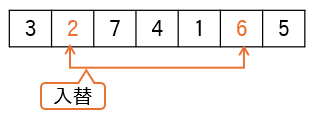
(3)該当する値が見つかったら、交換します。

5-2-7 トレース4

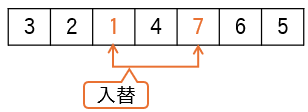
(4)探索を続け、さらに該当する値が見つかったら交換します。

5-2-7 トレース5

5-2-7 トレース6

(5)該当する値が無くなった時点で、配列の要素は基準値より小さいグループと大きいグループに分かれます。

5-2-7 トレース7

(6)それぞれのグループの部分配列を対象に、クイックソートの関数を再帰呼び出しします。

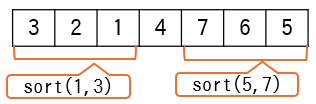
5-2-7 トレース8

(7)左部分の配列に対し、(1)(2)と同様の処理を行います。

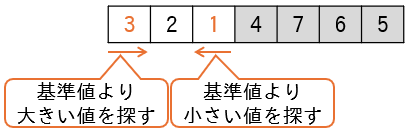
5-2-7 トレース9

結果として、左部分が昇順に並びます。

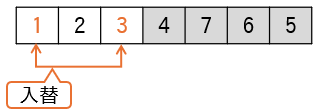
5-2-7 トレース10

(8)右部分の配列に対し、(1)(2)と同様の処理を行います。

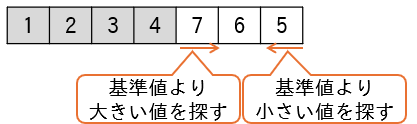
5-2-7 トレース11

結果として、右部分が昇順に並びます。

5-2-7 トレース12

ヒント1

問題の内容は初回の/*** α ***/の内容を答えるものです。クイックソートの動きを知らなくても最初のwhile文の動作を追うことができれば解答できます。

考え中

解答解説

〔解答〕

　エ

〔解説〕

プログラム序盤をトレースしてみましょう。まずは10～12行目の以下の処理です。

while (data[i] ＜ pivot)
  i ← i ＋ 1
endwhile

この処理は下図のように、配列の左側から基準より大きい値を探しています。

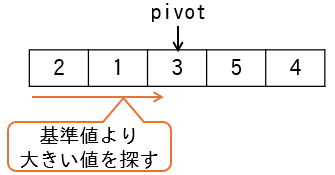
5-2-7 トレース13

トレース表は次のとおりです。

処理 i j pivot data 条件
while (data[i] ＜ pivot) 1 5 3 {2,1,3,5,4} true
　i ← i ＋ 1 2 5 3 {2,1,3,5,4}
while (data[i] ＜ pivot) 2 5 3 {2,1,3,5,4} true
　i ← i ＋ 1 3 5 3 {2,1,3,5,4}
while (data[i] ＜ pivot) 3 5 3 {2,1,3,5,4} false

基準値より大きい値は1つもないため、iがpivotに来た時点でループを抜けています。

次に13～15行目の以下の処理です。

while (pivot ＜ data[j])
  j ← j ー 1
endwhile

この処理は下図のように、配列の右側から基準より小さい値を探しています。

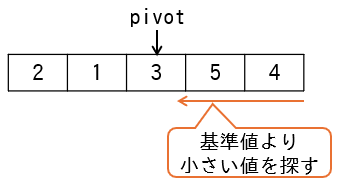
5-2-7 トレース13

トレース表は次のとおりです。

処理 i j pivot data 条件
while (pivot ＜ data[j]) 3 5 3 {2,1,3,5,4} true
　j ← j ー 1 3 4 3 {2,1,3,5,4}
while (data[i] ＜ pivot) 2 4 3 {2,1,3,5,4} true
　j ← j ー 1 3 3 3 {2,1,3,5,4}
while (data[i] ＜ pivot) 3 3 3 {2,1,3,5,4} false

基準値より小さい値は1つもないため、jがpivotに来た時点でループを抜けています。

トレースの続きを確認します。

処理 i j pivot data 条件
if (i ≧ j) 3 3 3 {2,1,3,5,4} true

if (i ≧ j)において条件式がtrueとなりますので、9～22行目の外側whileループを抜け、/*** α ***/の処理となります。この時点で配列dataは変化していませんので、初期状態と同じ 「2 1 3 5 4」 が出力されることになります。答えはエとなります。

答えはすでに出ていますが、トレースして続きの動作を見てみましょう。

処理 first end i j pivot data 条件
if (first ＜ i ー 1) 1 5 3 3 3 {2,1,3,5,4} true
　sort(first, i ー 1) 1 5 3 3 3 {2,1,3,5,4} -

再帰的に関数を呼び出すかを判定しています。条件式はtrueなので、 sort(1,2) で再帰呼び出しが行われます。

sort(1,2)の実行で、下図の部分配列をクイックソートしています。

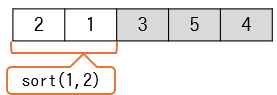
5-2-7 トレース15

ここからsort(1,2)のトレースです。

処理 first last i j pivot data 条件
pivot←data[(first+last)÷2の商] 1 2 - - 2 {2,1,3,5,4} -
i ← first 1 2 1 - 2 {2,1,3,5,4} -
j ← last 1 2 1 2 2 {2,1,3,5,4} -

pivot,i,jの値が決まります。

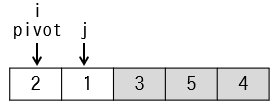
5-2-7 トレース17

処理 i j pivot data 条件
while (data[i] ＜ pivot) 1 2 2 {2,1,3,5,4} false
while (pivot ＜ data[j]) 1 2 2 {2,1,3,5,4} false

左右から入替対象の値を探していますが、該当するものがなく、変数i,jは変化しません。

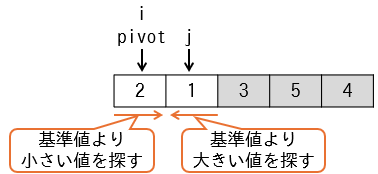
5-2-7 トレース18

処理 i j pivot data 条件
if (i ≧ j) 1 2 2 {2,1,3,5,4} false
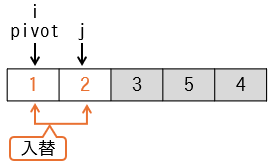
data[i]とdata[j]の値を入れ替える 1 2 2 {1,2,3,5,4} -

結果的に最初の要素と2番目の要素の入替が発生します。

5-2-7 トレース19

処理 i j pivot data 条件
i ← i + 1 2 2 2 {1,2,3,5,4} -
j ← j ー 1 2 1 2 {1,2,3,5,4} -
while (data[i] ＜ pivot) 2 1 2 {1,2,3,5,4} false
while (pivot ＜ data[j]) 2 1 2 {1,2,3,5,4} false
if (i ≧ j) 2 1 2 {1,2,3,5,4} false
dataの～出力する 2 1 2 {1,2,3,5,4} false

入替操作はこれ以上発生せず、再帰呼び出しが必要かの判定に入ります。

処理 first last i j pivot data 条件
if (first ＜ i ー 1) 1 2 2 1 3 {1,2,3,5,4} false
if (j ＋ 1 ＜ last) 1 2 2 1 3 {1,2,3,5,4} false

これ以上部分配列は存在しないため呼び出しは行われず、sort(1,2)による動作はこれで終了です。部分配列がソートされたことがわかります。

sort(1,5)に戻り、動作の続きを見ていきましょう。

処理 first last i j pivot data 条件
if (j ＋ 1 ＜ last) 1 5 3 3 3 {1,2,3,5,4} -
　sort (j ＋ 1, last) 1 5 3 3 3 {1,2,3,5,4} -

条件式はtrueなので、sort(4,5) で再帰呼び出しが行われます。この呼び出しでは下図の部分配列をクイックソートしています。

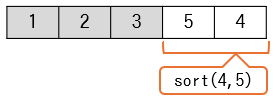
5-2-7 トレース16

sort(4,5)による動作は次のようになります。

処理 first last i j pivot data 条件
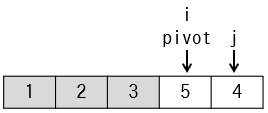
pivot←data[(first+last)÷2の商] 4 5 - - 5 {1,2,3,5,4} -
i ← first 4 5 4 - 5 {1,2,3,5,4} -
j ← last 4 5 4 5 5 {1,2,3,5,4} -

pivot,i,jの値が決まります。

5-2-7 トレース20

処理 i j pivot data 条件
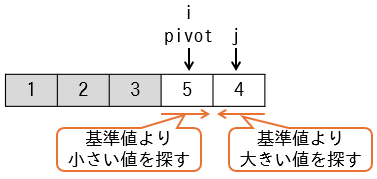
while (data[i] ＜ pivot) 4 5 5 {1,2,3,5,4} false
while (pivot ＜ data[j]) 4 5 5 {1,2,3,5,4} false

左右から入替対象の値を探していますが、該当するものがなく、変数i,jは変化しません。

5-2-7 トレース21

処理 i j pivot data 条件
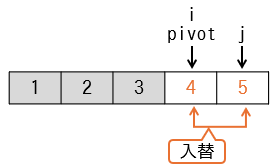
if (i ≧ j) 4 5 5 {1,2,3,5,4} false
data[i]とdata[j]の値を入れ替える 4 5 5 {1,2,3,4,5} -

ここで4番目の要素と5番目の要素の入替が発生しています。

5-2-7 トレース22

処理 i j pivot data 条件
i ← i + 1 5 5 5 {1,2,3,4,5} -
j ← j ー 1 5 4 5 {1,2,3,4,5} -
while (data[i] ＜ pivot) 5 4 5 {1,2,3,4,5} false
while (pivot ＜ data[j]) 5 4 5 {1,2,3,4,5} false
if (i ≧ j) 5 4 5 {1,2,3,4,5} true
dataの～出力する 5 4 5 {1,2,3,4,5} -

入替操作はこれ以上発生せず、再帰呼び出しが必要かの判定に入ります。

処理 first last i j pivot data 条件
if (first ＜ i ー 1) 4 5 5 4 5 {1,2,3,4,5} false
if (j ＋ 1 ＜ last) 4 5 5 4 5 {1,2,3,4,5} false

sort(4,5)による動作はこれで終了です。部分配列がソートされたことがわかります。

sort(4,5)が終わると共に、sort(1,5)も動作終了となります。すべての配列が昇順に整列されました。

おわりに

今回は以上となります。最後までご活用いただき、ありがとうございました。サーチとソートは数多く出題されるテーマで、複雑な処理を伴います。トレース力を問われる問題も多いので、ぜひトレースの練習をしながら学習を進めてみてください。

[PR]
ECFエデュケーションから、IPAの公開問題＋オリジナル問題5問も加えた充実の科目Bアルゴリズム対策問題集も販売中！kindle Unlimitedなら、全30問読み放題です。

基本情報技術者試験 科目B アルゴリズム対策問題集 令和7年版
AmazonでECFエデュケーションの基本情報技術者試験 科目B アルゴリズム対策問題集 令和7年版。アマゾンならポイント還元本が多数。一度購入いただいた電子書籍は、KindleおよびFire端末、スマートフォンやタブレットなど、様々な端末...
www.amazon.co.jp
タイトルとURLをコピーしました