こんにちは。ECF代表のヒガです。
本記事では初心者向けアルゴリズムの演習問題を紹介しています。日頃のプログラミング学習にご活用ください。
はじめに
アルゴリズムとは、コンピューターに行わせる計算手順のことです。自在にプログラムを作るには、プログラム言語の文法の知識とともにアルゴリズムの考え方を身につけることが必要になります。
アルゴリズム技法習得の肝は「繰り返し」の活用です。この連載では、簡単な題材で繰り返しを使うアルゴリズムの基本パターンを練習していきます。
演習問題の一覧や勉強スタイルについてのアドバイスはこちらからどうぞ。

[PR]
本連載について、実装例をPythonとしたKindle本も発売中です。Pythonで勉強中、タブレットで表示させたい、など、ご自身の状況に合わせてご活用ください。

Q033 配列データから目的のデータを探す(線形探索)
文字列型の配列に格納された複数の文字列データについて、指定した文字列(探索キー)の格納位置(添字)を表示させてください。なお、指定の文字列が配列の文字列データに含まれない場合は文字列「Not found」を表示させてください。
初期値として {"abc", "abcd", "abcde", "xx", "yyy"} を使って文字列型(JavaではString型)配列を準備し、さらに探索キーとして「abcde」を指定した場合の実行例は次のとおりです。
配列で文字列"abcde"が格納されている要素の添字「2」が表示されます。
同じ配列データで、探索文字列として「ab」を指定した場合の実行例は次のとおりです。
配列に該当データが無いので、「Not found」というメッセージが表示されます。
データ探索には様々なアルゴリズムがすでに考え出されていますが、今回は線形探索(逐次探索)を使ってください。詳細は以下で説明します。
線形探索
数あるデータ探索アルゴリズムのなかで、最も基本的かつ代表的なアルゴリズムです。やることは難しくなく、素朴に「データ列を前から順番に確認していく」アルゴリズムとなります。
具体的には、配列データについて
- 1番目の要素と探索キーが一致するか確認する
- 一致すれば探索成功、一致しなければ探索を続ける
- 2番目の要素と探索キーが一致するか確認する
- 一致すれば探索成功、一致しなければ探索を続ける
・・・
といった感じで、一致する・しないの判断を配列の最後まで繰り返していきます。探索成功のときはその時点で繰り返しを終了し、今回の場合であれば添字の表示処理を行います。配列の最後まで繰り返しを行っても探索成功とならない場合は、探索失敗を意味し、「Not found」を表示します。
ヒント
上記の線形探索の説明を具体的にフローチャートやプログラムに落とし込みましょう。全体としては以下の3段階になります。
- 配列、変数の準備
- 探索ループ
- 該当添字または「Not Found」の表示
また、Javaでは文字列の比較にはequals()メソッドを使います。具体的な使い方はJavaの解説書や解説サイトを参照ください。他のプログラム言語でも、文字列の比較の方法について不安がある方は、一度解説書や解説サイトを確認してから演習を進めてください。
解答例と解説
考え方
まずは今回の主題である線形探索の探索ループを考えてみましょう。ループということで、まず最初に「何を繰り返す」かを考えます。今回の場合は
- 配列のデータ要素と探索キーが等しいか判断する
を繰り返すことになります。もし等しければ探索成功(繰り返しを終了)、等しくなければ次の繰り返しに進むことになります。
箇条書きでまとめると、
- 次の動作を配列の要素数の分繰り返す
- 【カウンタ変数】番目のデータ要素と探索キーを比較する
- 一致する場合、繰り返しを抜ける
- 【カウンタ変数】番目のデータ要素と探索キーを比較する
という流れになります。
続けて、探索ループ後の表示部分を考えます。
探索ループが終わるには2つのパターンがあることになります。
- 探索成功し、該当の添字が確定している
- 繰り返しが最後まで行われる(探索失敗)
です。この2パターンについて条件分岐で表示を変えることになります。
配列の添字は探索ループのカウンタ変数と対応していますが、探索が失敗して繰り返しを最後まで行うと、このカウンタ変数が「配列最後の要素の添字+1」になっているはずです。繰り返しの終了条件がそうなっているためです。逆に、探索に成功した場合はカウンタ変数は「配列最後の要素の添字以下」の数になっています。条件分岐で行う表示内容を含め、箇条書きでまとめましょう。
- 【カウンタ変数】が【配列最後の要素の添字】以下か
- 真(探索成功)の場合、【カウンタ変数】(添字)を表示
- 偽(探索失敗)の場合、文字列"Not found"を表示
となります。
最後に全体をまとめます。
- 次の動作を配列の要素数の分繰り返す
- 【カウンタ変数】番目のデータ要素と探索キーを比較する
- 一致する場合、繰り返しを抜ける
- 【カウンタ変数】番目のデータ要素と探索キーを比較する
- 1の繰り返しの【カウンタ変数】が【配列最後の要素の添字】以下か
- 真(探索成功)の場合、【カウンタ変数】(添字に対応)を表示
- 偽(探索失敗)の場合、文字列"Not found"を表示
フローチャート例
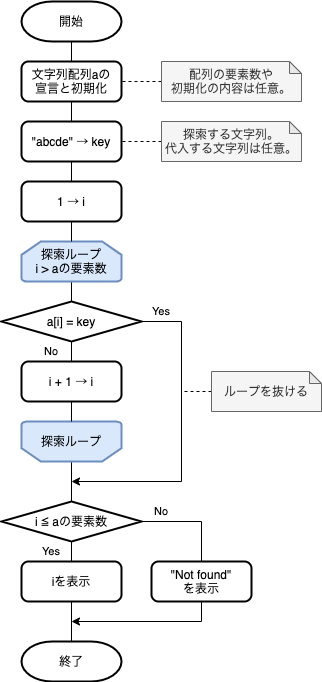
探索ループは「データ要素と探索キーが等しいか?」の条件分岐を繰り返す、という形になっています。探索ループが終わると添字表示のための条件分岐を行います。
Javaでの実装例
public class Q033 {
public static void main(String[] args) {
String[] a = {"abc", "abcd", "abcde", "xx", "yyy"}; // 操作対象配列の宣言と初期化
String key = "abcde"; // 探索キー(見つかる場合)
//String key = "ab"; // 探索キー(見つからない場合)
int i; // カウンタ変数(=見つかった要素の添字)
for (i = 0; i < a.length; i++) { // 探索ループ
if (a[i].equals(key)) {
break;
}
}
if (i < a.length) { // 見つかったか
System.out.println(i);
} else {
System.out.println("Not found");
}
}
}
Javaでは配列の添字は「0」からスタートしますので、カウンタ変数iの初期化や継続条件式は、上記のフローチャートからはそのように変更しています。配列の要素の添字は0から4(要素数 - 1)なので、0から4までの5回の繰り返しです。
今回、8行目でカウンタ変数iの宣言を行っています。初期化(i = 0)はいつもどおりfor文の中です。Javaでは、ローカル変数はその宣言したブロックの中だけしか使えないという決まりがあります。今回は変数iを15行目以降の条件分岐の条件や表示に使う必要がありますので、宣言をfor文の外で行いました。
おわりに
本連載ではプログラムで使える基本的なアルゴリズムのパターンを練習してきたのですが、実は開発業界人との会話で「アルゴリズムを勉強する」と言うときには、「データの探索」や「データの並び替え」、「データ構造の実現」のような、具体的なアプリケーショションの機能として使う処理について、先人たちが考えたアルゴリズム群を勉強することを指すことが多いです。実践では、この勉強したアルゴリズムの中から目的に合ったアルゴリズムを選び、直接活用することを目的としています。
皆さんも初心者とはいえ、そろそろ基本的なアルゴリズムの考え方にも慣れてきた頃だろうということで、今回からこの「先人たちから受け継がれたアルゴリズム」の紹介を行っていきます。問題設定が具体的になったと言うだけで、中身はこれまでと同じ様に「繰り返し」です。
今回は探索アルゴリズムの一つ、線形探索について勉強しました。「探索」はつまり「検索」です。Webの検索は日常ですし、様々なアプリケーションには検索機能が備わっています。線形探索アルゴリズムは効率が悪く、大量のデータを扱うシステムでは使いづらいのですが、まずは基本として押さえておく必要があります。他にどんな探索アルゴリズムがあるかは、自身の課題として調べてみましょう。
次回はこちらです。

[PR]

