こんにちは。ECF代表のヒガです。
本記事では初心者向けアルゴリズムの演習問題を紹介しています。日頃のプログラミング学習にご活用ください。
はじめに
アルゴリズムとは、コンピューターに行わせる計算手順のことです。自在にプログラムを作るには、プログラム言語の文法の知識とともにアルゴリズムの考え方を身につけることが必要になります。
アルゴリズム技法習得の肝は「繰り返し」の活用です。この連載では、簡単な題材で繰り返しを使うアルゴリズムの基本パターンを練習していきます。
演習問題の一覧や勉強スタイルについてのアドバイスはこちらからどうぞ。

[PR]
本連載について、実装例をPythonとしたKindle本も発売中です。Pythonで勉強中、タブレットで表示させたい、など、ご自身の状況に合わせてご活用ください。

Q032 指定範囲のデータのみ合計
配列に格納された数値データのうち、指定の範囲に含まれるデータのみの合計を求め表示させてください。ただし、操作対象の配列はプログラムの先頭で宣言し、適当な初期値を代入してください。また、範囲の最小値と最大値についても、プログラムの先頭でそれぞれ変数に代入することで指定してください。
初期値として {68, 55, 72, 93, 87} を使って整数型(Javaではint型)配列を準備し、さらに最小値に「80」、最大値に「100」を指定した場合の実行例は次のとおりです。
80から100の間に含まれる「93」と「87」が合計の対象となります。
ヒント
合計アルゴリズム自体はQ030「配列データの合計」そのままです。しかし今回はその合計の対象が判断により限定されているということです。
解答例と解説
考え方
合計アルゴリズムについて、解説の詳細はQ030を参照しましょう。

今回も「何を繰り返す」かは、
- ここまでの合計と配列のデータ要素を足す(ただし【ここまでの合計】の初期値は0)
を繰り返すことになります。ただし今回は無条件に合計していくわけではありません。指定の範囲内のものだけです。つまり、指定の最小値・最大値で表現した条件式で判断を行った上で表示を行います。全体を箇条書きでまとめると、
- 変数【ここまでの合計】を用意し、0で初期化する
- 次の動作を配列の要素数の分繰り返す
- 「指定の最小値≦【カウンタ変数】番目のデータ要素≦指定の最大値」となっているか
- 真(Yes)の場合、以下の処理を行う
- 【ここまでの合計】に【カウンタ変数】番目のデータ要素を足す
- 真(Yes)の場合、以下の処理を行う
- 「指定の最小値≦【カウンタ変数】番目のデータ要素≦指定の最大値」となっているか
- 【ここまでの合計】を表示する
という流れになります。
フローチャート例
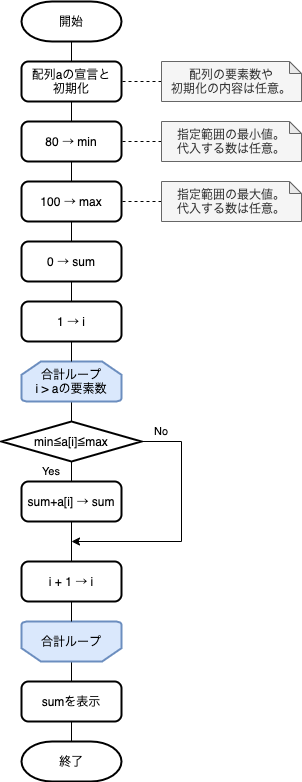
このフローチャートでは、配列の添字は「1」から始まるとしています。最後の要素の添字は配列の要素数と一致します。表示ループは、1から要素数まで(カウンタ変数iが要素数を超えたら終了)の繰り返しとなります。
データ要素を合計として加算する・しないの条件分岐を繰り返す、という形になっています。
Javaでの実装例
public class Q032 {
public static void main(String[] args) {
int[] a = {68, 55, 72, 93, 87}; // 操作対象配列の宣言と初期化
int min = 80; // 指定の範囲(最小)
int max = 100; // 指定の範囲(最大)
int sum = 0; // 合計格納用変数
for (int i = 0; i < a.length; i++) { // 合計ループ
if (min <= a[i] && a[i] <= max) {
sum = sum + a[i];
}
}
System.out.println(sum);
}
}
Javaでは配列の添字は「0」からスタートしますので、カウンタ変数iの初期化や継続条件式は、上記のフローチャートからはそのように変更しています。配列の要素の添字は0から4(要素数 - 1)なので、0から4までの5回の繰り返しです。
上のフローチャートとの対応からプログラム実装例の流れを確認しましょう。
おわりに
Q030「データの合計」とQ028「処理の対象データが条件で決まる繰り返し」の組み合わせパターンでした。そういう意味では新しいパターンではないのですが、似たような演習問題を行うことは知識の定着につながります。
本連載の演習問題の数はそれほど多いわけではないのですが、一つ一つの問題から皆さん自身で派生を考えて演習を進めることで、50本でも100本でも練習ができるでしょう。難しいことを考える必要は全くありません。数値を変える、配列の型を変える、条件を変える、など、気軽に変えられる部分を探してみてください。
次回はこちらです。

[PR]

