こんにちは。ECF代表のヒガです。
本記事では初心者向けアルゴリズムの演習問題を紹介しています。日頃のプログラミング学習にご活用ください。
はじめに
アルゴリズムとは、コンピューターに行わせる計算手順のことです。自在にプログラムを作るには、プログラム言語の文法の知識とともにアルゴリズムの考え方を身につけることが必要になります。
アルゴリズム技法習得の肝は「繰り返し」の活用です。この連載では、簡単な題材で繰り返しを使うアルゴリズムの基本パターンを練習していきます。
演習問題の一覧や勉強スタイルについてのアドバイスはこちらからどうぞ。
Q036 配列データの並び替え（選択法）
本連載「アルゴリズム入門 演習問題集 〜 繰り返しをマスターしよう！」の最終回となります。総まとめの問題です。
配列に格納された複数の数値データについて、数の小さい順（昇順）になるように並び替えてください。確認のために、並び替えの前後で配列データを表示させてください
初期値として {68, 55, 72, 93, 87} を使って整数型（Javaではint型）配列を準備した場合の実行例は次のとおりです。
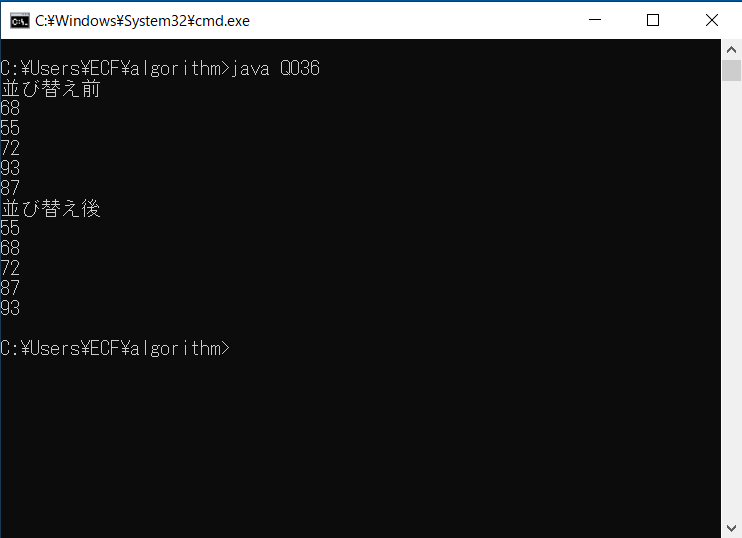
配列データの表示についてはQ024を参照してください。
データの並び替え（整列、ソート）には様々なアルゴリズムがすでに考え出されていますが、今回は選択法（選択ソート）を使ってください。詳細は以下で説明します。
選択法
数ある整列アルゴリズムのなかで、最も基本的かつ代表的なアルゴリズムです。簡単に表現すると、「配列データから最小値を探して前に移動させる」ことを繰り返していきます。
トランプゲームでの手札の並び替えをイメージするとわかりやすいかもしれません。皆さんは次のような手順で手札を並べることはありませんか。
- 全体から一番小さい数のカードを探す
- 見つけたら左側に移動する
- 残りのカードから一番小さいカードを探す
- 見つけたら左から2番目に移動する
- 残りのカードから一番小さいカードを探す
- 見つけたら左から3番目に移動する
- 以上の手順を最後まで繰り返していく
この手順を行うと、手札の左側からどんどんカードが並んでいく様子が見えるかと思います。似たような考え方で、選択法のアルゴリズムでは先頭からどんどん並び替えを確定させていきます。
配列データについて具体的に考えましょう。配列だとカードのように簡単に順番を変更できないので、もう一工夫が必要です
- 区間「1番目の要素から最後の要素まで」から最小値を探す
- 最小値の要素を1番目の要素と入れ替える（最小値を先頭に持ってくる）
- 区間「2番目の要素から最後の要素まで」から最小値を探す
- 最小値の要素を2番目の要素と入れ替える（最小値を先頭に持ってくる）
- 区間「3番目の要素から最後の要素まで」から最小値を探す
- 最小値の要素を3番目の要素と入れ替える（最小値を先頭に持ってくる）
・・・
といった感じで、「残り区間から最小値を探す・区間の先頭に持ってくる」を繰り返します。区間の先頭に持ってくるときは、もともとそこに格納されていたデータが上書きされて消えないように、最小値があった場所のデータと入れ替えを行うのがポイントです。
ヒント
上記の選択法の説明を具体的にフローチャートやプログラムに落とし込みましょう。
「最小値を探す＆入れ替える」を繰り返すことになりますが、最小値を探すときも繰り返しですので、繰り返しの繰り返し、二重ループとなります。2つのカウンタ変数をうまく使って配列要素を指定する必要があります。
二重ループの基本についてはこちらです。
最小値を探すアルゴリズムはこちらです。
変数の値を入れ替えるスワップ処理についてはこちらです。
解答例と解説
考え方
上記のヒントより「何を繰り返す」かを考えます。今回の場合は
- 指定区間から最小値を探す
- 最小値のデータ要素を区間の先頭のデータ要素と入れ替える
を繰り返すことになります。便宜上、ここではこの繰り返しを「整列確定ループ」と呼ぶことにします。
繰り返しの中で、並び替えが配列の先頭から順に済んでいきますので、指定区間の先頭は繰り返しの度に変化していきます。つまり、
- 1回目の繰り返しは1番目の要素から最後の要素まで
- 2回目の繰り返しは2番目の要素から最後の要素まで
- 3回目の繰り返しは3番目の要素から最後の要素まで
- ・・・
という形の変化です。整列確定ループのカウンタ変数そのままで指定区間の先頭が表現できることがわかります。
ここまでを箇条書きでまとめると、
- 次の動作を配列の要素数の分繰り返す（整列確定ループ）
- 【カウンタ変数】番目の要素から最後の要素の区間で最小値を探す
- 区間最小値の要素と【カウンタ変数】番目の要素を入れ替える
という流れになります。
さて、「最小値を探す」アルゴリズムも繰り返しで実現します。解説の詳細はQ034を参照するとして、とりあえず箇条書きを再掲します。
- 配列の1番目のデータ要素を暫定最小値とする（値やその添字を管理する）
- 次の動作を配列の2番目の要素から最後の要素まで繰り返す
- 暫定最小値と【カウンタ変数】番目のデータ要素を比較する
- 【カウンタ変数】番目のデータ要素が小さい場合、暫定最小値（値やその添字）を更新する
- 暫定最小値と【カウンタ変数】番目のデータ要素を比較する
この箇条書きは、配列の先頭（1番目）から最後までの区間での最小値探索を表現しています。今回は配列の指定区間から最小値を探すことになります。上で説明したとおり、指定区間は整列確定ループのカウンタ変数で表せました。具体的には「【カウンタ変数】番目の要素から最後の要素の区間」です。
それでは、整列確定ループのカウンタ変数をi、最小値探索ループのカウンタ変数をjとして書き換えます。指定区間は「i番目の要素から最後の要素の区間」となりますので、最小値探索アルゴリズムに当てはめると、
- 配列のi番目のデータ要素を暫定最小値とする
- 次の動作を配列のi+1番目の要素から最後の要素まで繰り返す（最小値探索ループ）
- 暫定最小値とj番目のデータ要素を比較する
- j番目のデータ要素が小さい場合、暫定最小値を更新する
- 暫定最小値とj番目のデータ要素を比較する
と表現できます（区間の先頭は暫定最大値の初期値、2番目から繰り返しを始める）。対応付けがうまくできるでしょうか。
それでは最後に、整列確定ループや区間最小値入れ替え処理を含める形で全体をまとめます。
- 次の動作を配列の要素数の分繰り返す（整列確定ループ）
- 配列のi番目のデータ要素を暫定最小値とする
- 次の動作を配列のi+1番目の要素から最後の要素まで繰り返す（最小値探索ループ）
- 暫定最小値とj番目のデータ要素を比較する
- j番目のデータ要素が小さい場合、暫定最小値を更新する
- 暫定最小値とj番目のデータ要素を比較する
- 区間最小値のデータ要素とi番目のデータ要素を入れ替える
箇条書きの最終形を見ると、二重ループとなっていて非常に込み入っているのですが、一つ一つの役割をまとまりとして理解できれば見通しが良くなると思います。
なお、この前後で確認用の配列表示も行いますが、こちらの解説は省略します（Q024を参照）。
フローチャート例
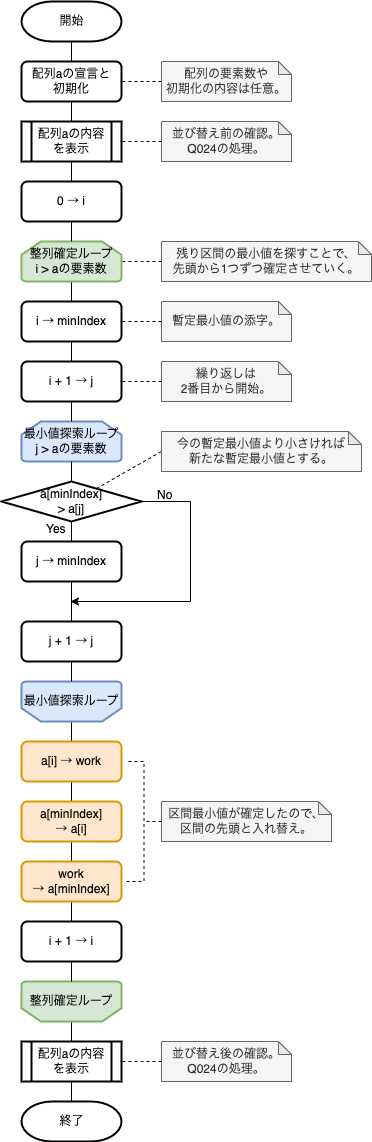
今回のフローチャート例では、Q034とは違い、暫定最小値は添字だけを管理しています（最小値の値そのものの管理は不要）。
実は、このフローチャート例では少しだけ無駄な処理が残っています。完成形から改めてトレース（具体的なデータを入れて流れを順にたどっていく）ことで見えてくると思いますので、発展課題として効率改善に是非チャレンジしてみてください。
Javaでの実装例
public class Q036 {
public static void main(String[] args) {
int[] a = {68, 55, 72, 93, 87}; // 操作対象配列の宣言と初期化
System.out.println("並び替え前");
for(int i = 0; i < a.length; i++) { // 操作対象配列内容の表示
System.out.println(a[i]);
}
for (int i = 0; i < a.length; i++) { // 整列確定ループ
int minIndex = i; // 暫定最小値の添字
for (int j = i + 1; j < a.length; j++) { // 最小値探索ループ
if (a[minIndex] > a[j]) { // 暫定最小値より小さいか
minIndex = j; // 暫定最大値の添字を更新
}
}
// 区間先頭の要素と区間最小値の要素を交換する
int work = a[i];
a[i] = a[minIndex]; // 区間最小値を区間先頭に移動
a[minIndex] = work;
}
System.out.println("並び替え後");
for(int i = 0; i < a.length; i++) { // 操作対象配列内容の表示
System.out.println(a[i]);
}
}
}
Javaでは配列の添字は「0」からスタートしますので、カウンタ変数iの初期化や継続条件式は、上記のフローチャートからはそのように変更しています。配列の要素の添字は0から4（要素数 - 1）なので、0から4までの5回の繰り返しです。
上のフローチャート例でも指摘しましたが、実は、この実装例では少しだけ無駄な処理が残っています。完成形から改めてトレース（具体的なデータを入れて流れを順にたどっていく）ことで見えてくると思いますので、発展課題として効率改善に是非チャレンジしてみてください。
おわりに
本連載の最終回は整列アルゴリズムの代表「選択法（選択ソート）」の紹介でした。総まとめということで、ここまでで一番難しかったと思います。
しかし、改めて完成形を眺めてみると、一つ一つの要素はこれまで行ってきた演習問題のパターンだということがわかると思います。簡単なアルゴリズムのパターンの組み合わせで複雑なアルゴリズムでも十分に表現できるということです。
アルゴリズムの勉強は確かに難しいのですが、まずは本連載で紹介した基本パターンが身につくよう、しっかり練習しましょう。その上で具体的な探索アルゴリズムや整列アルゴリズムを勉強すると、理解の進み具合が以前と違うことを感じられるはずです。ぜひ頑張ってください！
合同会社イー・シー・エフでは、子ども向けプログラミングなどの教育講座を実施しています。プログラミング教室の案内や教育教材の情報、また関連するご相談・問い合わせにつきましては下記よりご確認ください。
