こんにちは。ECF代表のヒガです。
はじめに
アルゴリズムとは、コンピューターに行わせる計算手順のことです。自在にプログラムを作るには、プログラム言語の文法の知識とともにアルゴリズムの考え方を身につけることが必要になります。
アルゴリズム技法習得の肝は「繰り返し」の活用です。この連載では、簡単な題材で繰り返しを使うアルゴリズムの基本パターンを練習していきます。
演習問題の一覧や勉強スタイルについてのアドバイスはこちらからどうぞ。

[PR]
本連載について、実装例をPythonとしたKindle本も発売中です。Pythonで勉強中、タブレットで表示させたい、など、ご自身の状況に合わせてご活用ください。

Q011 逆さの三角形に文字を並べる
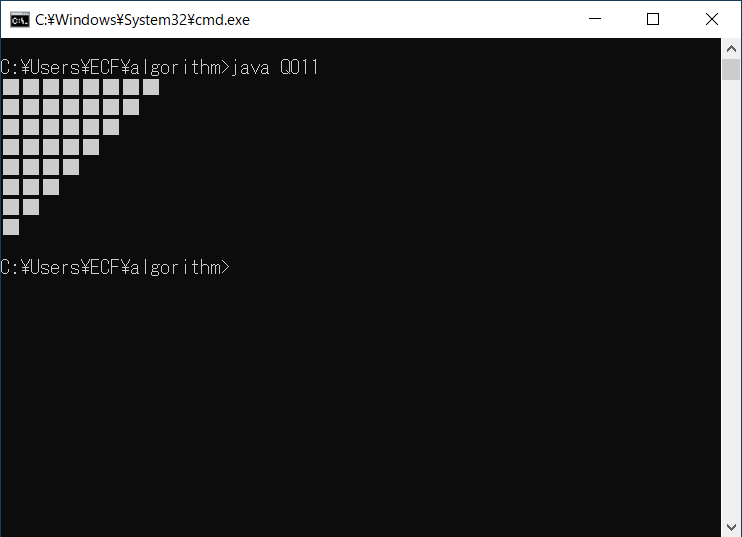
複数行にわたり数を1つずつ減らしながら文字「■」を表示することで、実行例のような三角形を表示させてください。ただし、行数(=列数)はプログラムの先頭で変数に代入することで指定してください。
行数に「8」を指定した場合の実行例は次のとおりです。
ヒント
Q005の基本の二重ループの応用です。また、Q010の修正版でもあります。違いは、列ループ内の繰り返し回数について指定数回から1回まで適切に変化させる必要があります。
解答例と解説
考え方
ベースとなるのは基本の二重ループですので、とりあえず箇条書きにまとめた
- 行数と列数(繰り返し回数)を指定する
- 次の動作を行数分繰り返す
- 次の動作を列数分繰り返す
- 文字'■'を表示する
- 改行する
- 次の動作を列数分繰り返す
をスタート地点としましょう。

今回変わってくるのは、太字で書かれた小さな繰り返しの「列数分」の条件です。具体的に行数に「8」を指定したときの、繰り返し数を考えてみましょう。
| i行目 | 表示する文字数(=繰り返し数) |
|---|---|
| 1 | 8 |
| 2 | 7 |
| 3 | 6 |
| 4 | 5 |
| 5 | 4 |
| 6 | 3 |
| 7 | 2 |
| 8 | 1 |
関係性が見えてきたでしょうか。規則性は明確ですが、Q010と違い、i行目と文字数の関係性は少しわかりにくいですね。
ループ変数iが増えていくに連れ減っていく値は、「全体の繰り返し回数 - i」を使って計算するのが定石となっています。これはしっかり理解し、覚えておきたいテクニックです。先程の表に関係式を追加してみます。
| i行目 | 表示する文字数(=繰り返し数) | iとの関係式 |
|---|---|---|
| 1 | 8 | 8 - 1 + 1 = 8 |
| 2 | 7 | 8 - 2 + 1 = 7 |
| 3 | 6 | 8 - 3 + 1 = 6 |
| 4 | 5 | 8 - 4 + 1 = 5 |
| 5 | 4 | 8 - 5 + 1 = 4 |
| 6 | 3 | 8 - 6 + 1 = 3 |
| 7 | 2 | 8 - 7 + 1 = 2 |
| 8 | 1 | 8 - 8 + 1 = 1 |
指定行数の「8」からiを引き、調整で1を足しました。これが関係式です。
それでは箇条書きを更新してみましょう。
- 行数と列数(繰り返し回数)を指定する
- 次の動作を行数分繰り返す
- 次の動作を「指定回数 - 行番号i + 1」回繰り返す
- 文字'■'を表示する
- 改行する
- 次の動作を「指定回数 - 行番号i + 1」回繰り返す
となります。
フローチャート例
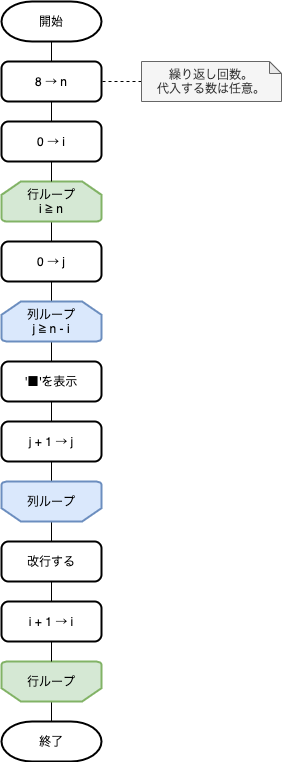
プログラム実装を意識した都合で、行ループの開始が「0回目」から始まっています。 考え方で示した表を改めて書き直すと、具体的に行数に「8」を指定したとき、
| i行目 | 表示する文字数(=繰り返し数) | iとの関係式 |
|---|---|---|
| 0 | 8 | 8 - 0 = 8 |
| 1 | 7 | 8 - 1 = 7 |
| 2 | 6 | 8 - 2 = 6 |
| 3 | 5 | 8 - 3 = 5 |
| 4 | 4 | 8 - 4 = 4 |
| 5 | 3 | 8 - 5 = 3 |
| 6 | 2 | 8 - 6 = 2 |
| 7 | 1 | 8 - 7 = 1 |
となります。文字数は指定行数の「8」からiを引いた数で計算できました。ということで、列ループの終了条件は変数nを使い、そのように直しています。
Javaでの実装例
public class Q011 {
public static void main(String[] args) {
int n = 8; // 繰り返しの数
for (int i = 0; i < n; i++) { // 行ループ
for (int j = 0; j < n - i; j++) { // 列ループ
System.out.print('■');
}
System.out.println(); // 列ループが終われば改行
}
}
}
上のフローチャートとの対応からプログラム実装例の流れを確認しましょう。
おわりに
今回はQ010とはまた別パターンのカウンタ変数の使い方を紹介しました。繰り返しの数(今回の変数n)もまた繰り返し内での計算式や条件式の構成に便利に使えますので、しっかり今回の例を理解して活用していきましょう。
次回はこちらです。

[PR]

